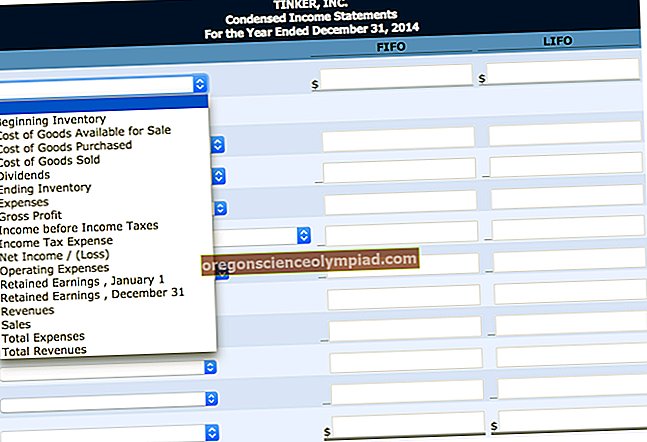
Tavaline annuiteet on maksete jada, mis tehakse iga perioodi lõpus maksete jadas. Levinud finantsplaneerimise kontseptsioon on arvutada rahasumma, mis makstakse investorile tagasi tulevikus, kui investor teeb enne seda kuupäeva rea makseid, eeldades, et vahendid on investeeritud kindla intressimääraga. Tulevikuväärtus on kindlal kuupäeval tulevikus makstava sularaha summa väärtus. Seetõttu viitab tavalise annuiteedi tulevase väärtuse valem perioodiliste maksete rea väärtusele konkreetsel tuleviku kuupäeval, kus iga makse tehakse perioodi lõpus.
Tavalise annuiteedi tulevase väärtuse arvutamise valem (kui mitme perioodi lõpus tehakse rida võrdseid makseid) on järgmine:
P = PMT [((1 + r) n - 1) / r]
Kus:
P = tulevikus makstava annuiteetvoo tulevane väärtus
PMT = iga annuiteetmakse summa
r = intressimäär
n = perioodide arv, mille jooksul makseid tehakse
See väärtus on summa, milleni tulevaste maksete voog kasvab, eeldades, et teatud periood liitintressitulu koguneb mõõteperioodi jooksul järk-järgult. Tavaliselt on võrrandi võtmemuutujaks intressimäära eeldus, mille võib tulevastes perioodides tegelikult kogetavast intressimäärast tõsiselt kõrvale jätta.
Näiteks loodab ABC Internationali laekur investeerida järgmise viie aasta jooksul iga aasta lõpus 100 000 dollarit ettevõtte vahenditest pikaajalisse investeerimisvahendisse. Ta loodab, et ettevõte teenib 7% intressi, mis suureneb igal aastal. Väärtus, mis peaks neil maksetel olema viieaastase perioodi lõpus, arvutatakse järgmiselt:
P = 100 000 dollarit [((1 +, 07) 5 - 1) /, 07]
P = 575 074 dollarit
Teise näitena, mis oleks, kui investeeringu intress suureneks iga aasta asemel iga kuu ja investeeritud summa oleks kuu lõpus 8000 dollarit? Arvutus on järgmine:
P = 8 000 dollarit [((1 + .005833) 60 - 1) / .005833]
P = 572 737 dollarit
Viimases näites kasutatud .005833 intressimäär on 1/12 kogu 7% aastasest intressimäärast.